Calculating Wish
2012年2月15日 MTG - 電波系 コメント (4)
日付変わって一昨日投稿した新デッキ。構成もシンプルな上に、勝ち手段も確率計算に拠るところが大きいので、各カードの最適枚数を自分でも計算できるのではないかと生意気にも思い立つ。
さらには、MTG計算機という便利なスクリプトをご用意されているサイトを発見しつつ、利用させて頂きましたm(_ _)m
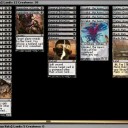
「確率」の計算は高校以来好んでやった記憶がないし、その点計算にあたっての考え方等々が間違っているかもしれないけれども、計算と実践を繰り返しつつ、現状完成したのが画像のレシピ。
コンボパーツは計算で確かめるまでもなく最適枚数が4枚なのは明らかなので、個人的に一番計算したかったのが秘匿ランド以外の土地の最適枚数。(2ターン目に1枚置くに最適な枚数は8枚 )
コジレックの審問の枠はマリガンした際の隙を補う必要有りという経験則からの投入であって、数学的な理由あって投入したわけではないのと、この点ネズミの総枚数の最適枚数との兼ね合いで、その枠を2枚削ることの許容性を検証する必要があると思ったところ、ネズミの総数:34枚というのも、結構理に適った数字だと思う。つまり、この場合、
という具合に、不思議と綺麗にまとまってくる。(その際、エムラが4枚ライブラリ-20枚に眠る場合におけるコンボ完成一歩手前の確率:80% / 3枚の場合:60% ⇒無論秘匿ランドがハンドにあることが前提)
上記はぶん回り中のぶん回りを前提にしているけれども、途中のフェッチ(計8枚)でライブラリーを1枚圧縮できること、不要カードを再度摘出/根絶(計8枚)できることを考えると、デッキのバランスを失わずにウケを広くできるという点で、均衡が保てた=最適枚数であるとも思える。
・・・外科的摘出が初手にあるか否か云々恐らく色々と場合分けをした上で、他にも色々と計算・検証しないと、数学的に正しいかどうかを確かめたことにはならないのだろうと思うし、そもそも、計算に際しての考え方が違っている可能性もあるけれども(^_^;)、現状、計算で導いた枚数と体感・経験則がおおよそ上手く合致できたかな、と自分に言い聞かせて思っています。
言うても、このデッキを使うと十中八九、相手が「!?」してくれるので、その点プレイしていても面白い。このデッキにあっては、回していて楽しければそれでいいのだ!(開き直り)
- 計算力を願ったが、それを運用するための知識と忍耐力が無かった
さらには、MTG計算機という便利なスクリプトをご用意されているサイトを発見しつつ、利用させて頂きましたm(_ _)m
「確率」の計算は高校以来好んでやった記憶がないし、その点計算にあたっての考え方等々が間違っているかもしれないけれども、計算と実践を繰り返しつつ、現状完成したのが画像のレシピ。
コンボパーツは計算で確かめるまでもなく最適枚数が4枚なのは明らかなので、個人的に一番計算したかったのが秘匿ランド以外の土地の最適枚数。(2ターン目に1枚置くに最適な枚数は8枚 )
コジレックの審問の枠はマリガンした際の隙を補う必要有りという経験則からの投入であって、数学的な理由あって投入したわけではないのと、この点ネズミの総枚数の最適枚数との兼ね合いで、その枠を2枚削ることの許容性を検証する必要があると思ったところ、ネズミの総数:34枚というのも、結構理に適った数字だと思う。つまり、この場合、
後手1ターン目>
初手にある期待値: 4枚 (4.53枚)
このとき残52枚のデッキ内にいるネズミの総数:34-4枚 = 30枚
ターンエンド時に外科的摘出を撃つ>
ライブラリー残り:52-30枚= 22枚
---------------------------------------------
2ターン目ドロー後>残21枚
3ターン目ドロー後>残20枚⇒秘匿条件を満たす
という具合に、不思議と綺麗にまとまってくる。(その際、エムラが4枚ライブラリ-20枚に眠る場合におけるコンボ完成一歩手前の確率:80% / 3枚の場合:60% ⇒無論秘匿ランドがハンドにあることが前提)
上記はぶん回り中のぶん回りを前提にしているけれども、途中のフェッチ(計8枚)でライブラリーを1枚圧縮できること、不要カードを再度摘出/根絶(計8枚)できることを考えると、デッキのバランスを失わずにウケを広くできるという点で、均衡が保てた=最適枚数であるとも思える。
・・・外科的摘出が初手にあるか否か云々恐らく色々と場合分けをした上で、他にも色々と計算・検証しないと、数学的に正しいかどうかを確かめたことにはならないのだろうと思うし、そもそも、計算に際しての考え方が違っている可能性もあるけれども(^_^;)、現状、計算で導いた枚数と体感・経験則がおおよそ上手く合致できたかな、と
言うても、このデッキを使うと十中八九、相手が「!?」してくれるので、その点プレイしていても面白い。このデッキにあっては、回していて楽しければそれでいいのだ!(開き直り)
- 計算力を願ったが、それを運用するための知識と忍耐力が無かった

コメント
画像をぱっと見てネズミデッキかと思ったら、ものすごい構築で脱帽しました!
参考にしたいのでリンクさせて頂きます。よろしくお願いしますm(_ _)m
初めまして。そう言って頂けるとありがたいですし、作った
甲斐がありました(^_^)
現在調整中につき、よろしければまた覗いてやって下さいm(_ _)m
これは面白いですね!ネズミにこんな使い方があったとは!
感動です!
こんばんは&コメント頂きましてどうもありがとうございます!
試合にも勝てるデッキにも仕上げていきたいところですが、根っこはひねくれたカジュアルプレイヤーなので、面白いというお言葉を頂戴することが一番嬉しかったりもします(笑)